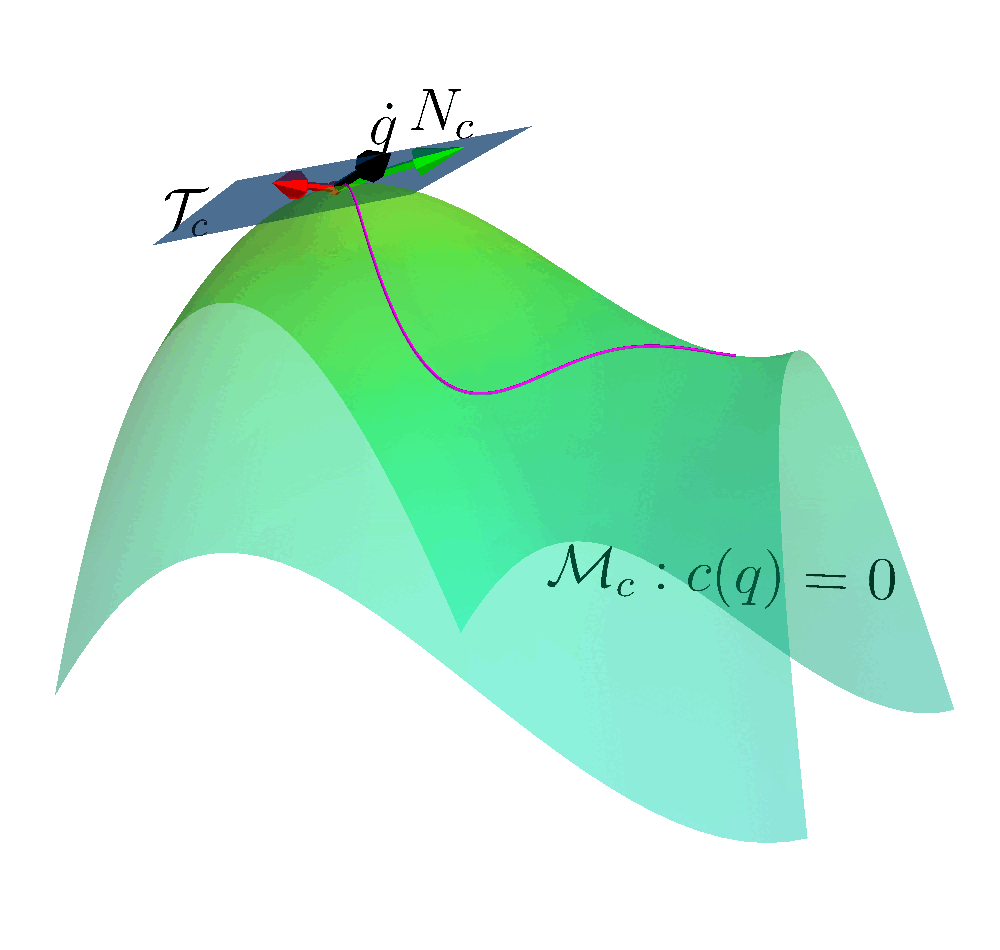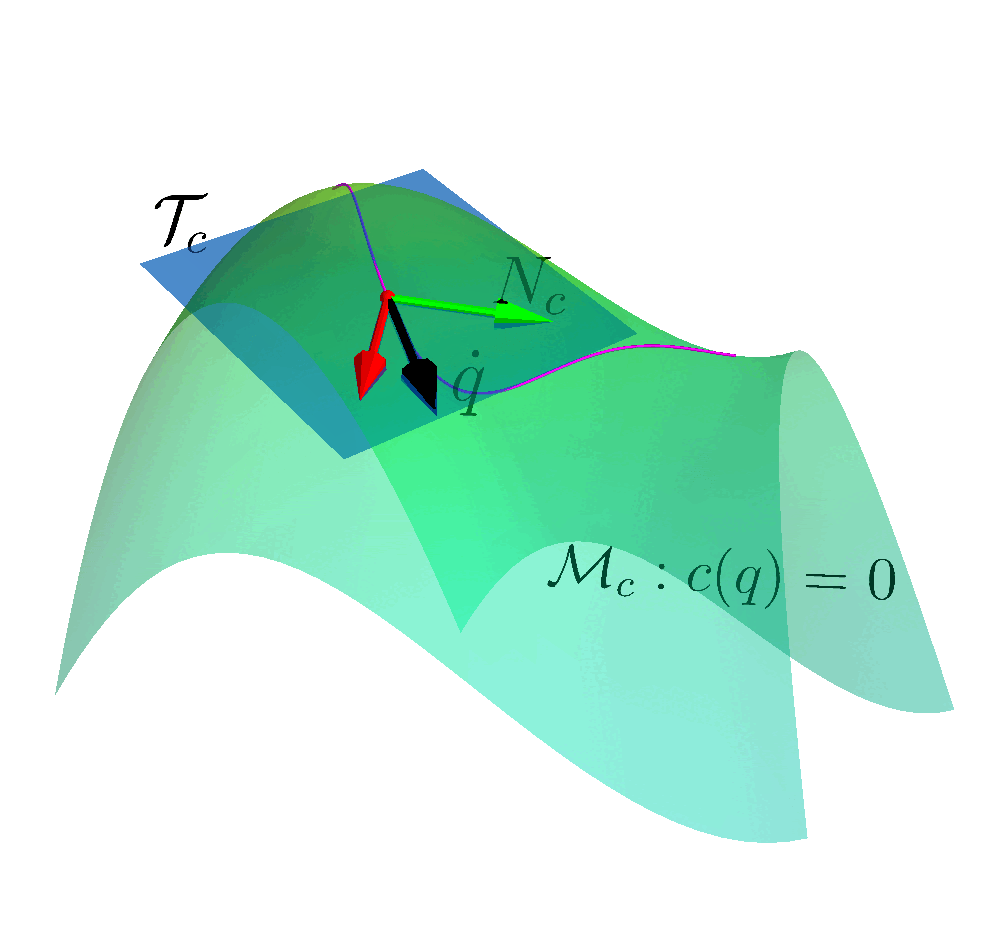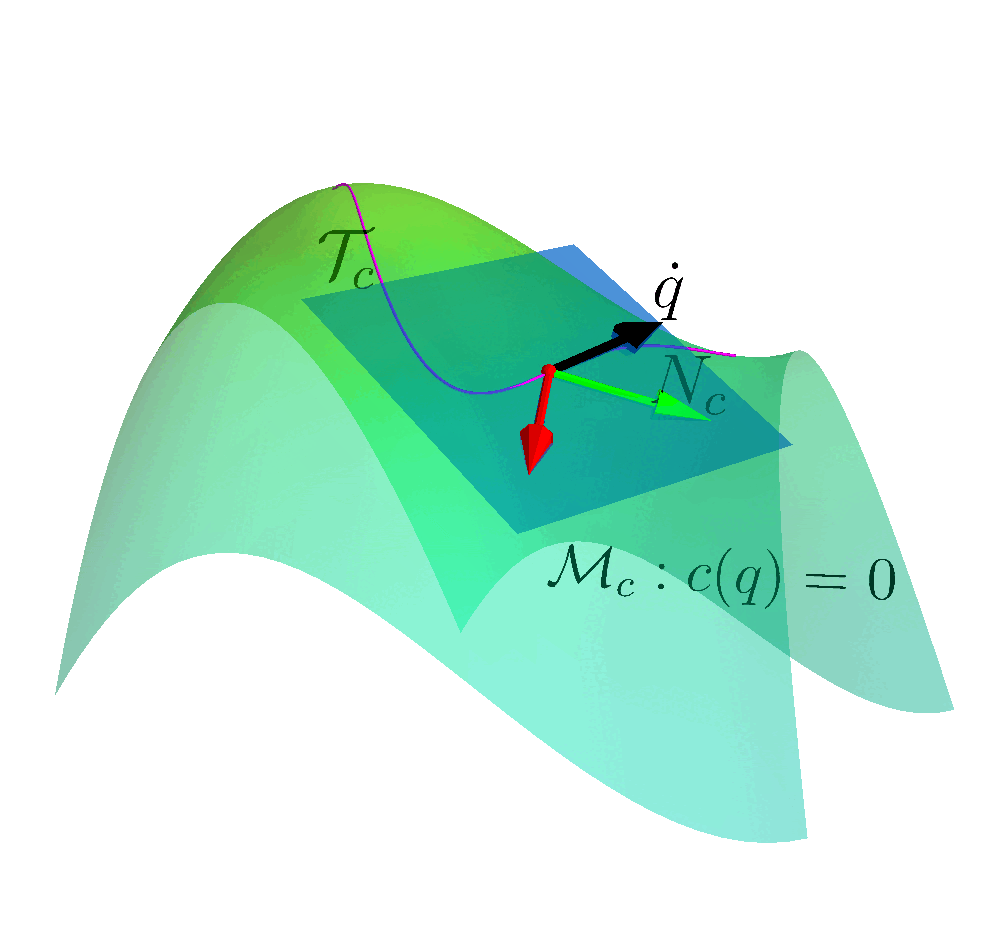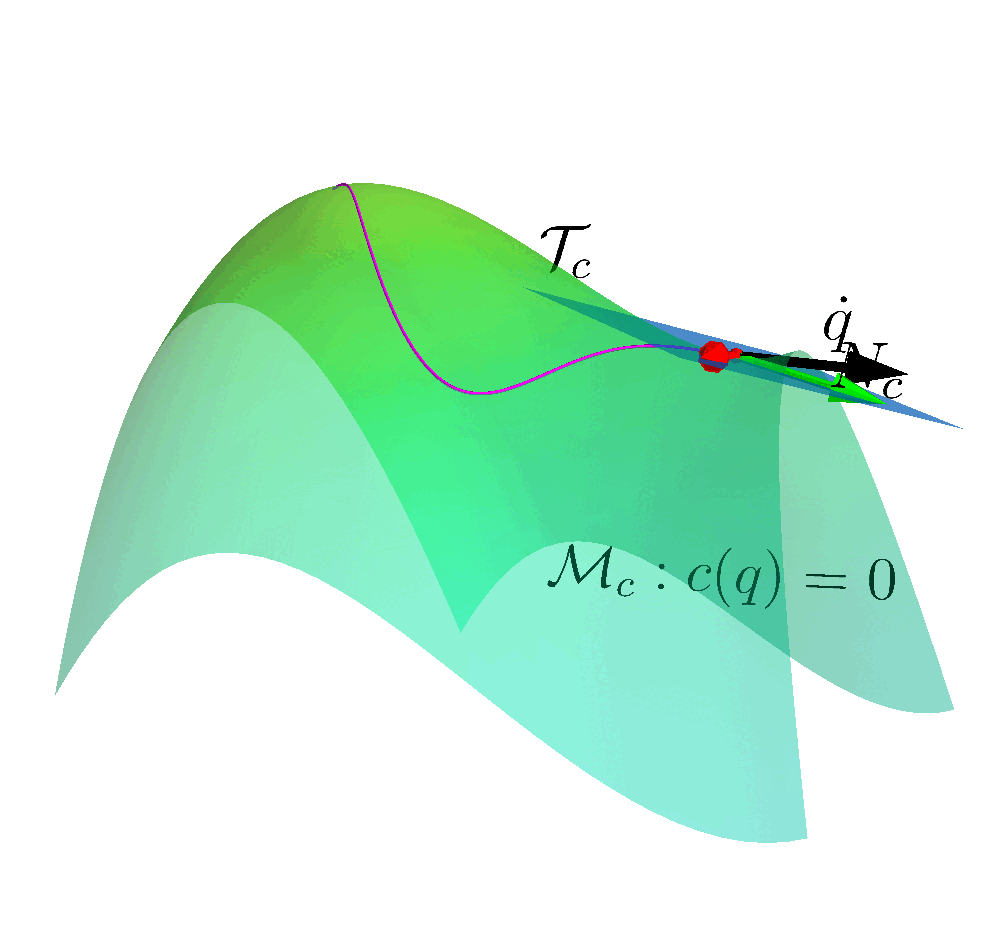
Code | Paper | Presentation

One of the biggest problems of deploying a reinforcement learning agent on a real robot platform is safety. One common formulation for safe reinforcement learning is CMDP, i.e., the accumulative discounted cost is smaller than a threshold $D$.

\[\begin{align*} \max \quad &\sum_{t=0}^{T}\gamma^t r(s_t, a_t)\\ \mathrm{s.t.} \quad &\sum_{t=0}^{T}\gamma^t c(s_t, a_t) < D \end{align*}\]

This problem focus on learning the final safe policy. However, this formulation is generally not applicable for safe-critical environment, such as, autonomous driving. There are several limitations in this formulation:

1. It’s hard to deal with multiple constraints.
2. For problems with big sim-to-real gap, deploying the final policy learned from simulation does not ensure safety.
3. Cumulative constraints may not reflect the safety when $c$ is not strictly positive or negative.
4. Safety is not guaranteed during the training process.

Safe Exploration

Instead, we consider the safe exploration problem as

\[\begin{align*} \max \quad &\sum_{t=0}^{T}\gamma^t r(s_t, a_t)\\ \mathrm{s.t.} \quad & c_i(s_t) \leq 0, \\ &\forall i\in [1,\cdots,N], t\in [0, \cdots, T] \end{align*}\]

This formulation ensures constraints satisfaction for multiple constraints $c_i$ at each individual step $t$.

To solve this problem, our idea is to construct a constraint manifold $\mathcal{M}= \{s: \bm{c}(s)=0\}$. The agent takes action which ensures the state on the manifold. In such way, we ensure the safety.

Sphere Manifold

Starting from a simple example, we can think about a unit sphere as a manifold embedded in 2D space: $\mathcal{M}_s=\{(x, y): x^2 + y^2 -1 = 0 \}$. For a point $p=(x_p, y_p)$ that stays on the manifold. We can compute its tangent vector. If we move the point along the tangent vector with an infinitesimal step. We ensure the point always stays on the sphere manifold.

Mathmatically, we can compute the derivate of the sphere function

\[J_s = \begin{bmatrix} 2x \\ 2y\end{bmatrix}\]

This vector is along the normal direction of the sphere, pointing outwards. The tangent vector (space) $N_s$ is perpendicular to vector $J_s$, i.e., null space. We can compute the null space via several numerical approaches, such as SVD and QR decomposition. The null space is

\(N_s = \text{Null}(J_s) = \begin{bmatrix}x \\ -y\end{bmatrix}\) Note that the tangent space is normalized. We can determine the state velocity to be aligned with the tangent vector

\[\begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} = N_s \alpha,\]

the state will move on the sphere manifold and $\alpha$ can be chosen arbitrarily.

If we consider the $\alpha$ as the action, all of the actions taken by the RL agent are safe.

Inequality Constraints

For most cases, the constraints are inequality constraints $\bm{c}(\bm{q})\leq \bm{0}, \bm{c}:\mathbb{R}^N\rightarrow \mathbb{R}^M$. We can construct the constraint manifold by introducing slack variables $\mu \in \mathbb{R}^M$.

\[\bar{\bm{c}}(\bm{q}, \bm{\mu}) = \bm{c}(\bm{q}) + \frac{1}{2}\bm{\mu}^2=0\]

In this way, we augment the original state space, the constraint manifold is embedded in $\mathbb{R}^{N+M}$. We can compute the Jacobian as

\[\bm{J}_c = \begin{bmatrix} \bm{J} \quad \text{diag}(\bm{\mu})\end{bmatrix}\]

and compute the null space as $\bm{N}_c = \text{Null}(\bm{J_c})$. Using this null space we can determine the safe action with any type of RL method.

Further details of the approach can be found in the paper.

_{[1] Puze Liu, Davide Tateo, Haitham Bou-Ammar, and Jan Peters, Robot Reinforcement Learning on the Constraint Manifold, In Proceedings of the 5th Conference on Robot Learning, vol. 164, pp. 1357–1366, 2022}

@inproceedings{CORL_2021_Learning_on_the_Manifold,
  title     = {Robot Reinforcement Learning on the Constraint Manifold},
  author    = {Liu, Puze and Tateo, Davide and Bou-Ammar, Haitham and Peters, Jan},
  booktitle   = {Proceedings of the 5th Conference on Robot Learning},
  pages       = {1357--1366},
  year        = {2022},
  editor      = {Faust, Aleksandra and Hsu, David and Neumann, Gerhard},
  volume      = {164},
  series      = {Proceedings of Machine Learning Research},
  publisher   = {PMLR},
}